The Physics of the Tesla Magnifying Transmitter, and the Transmission of Electrical Power Without Wires

ABSTRACT

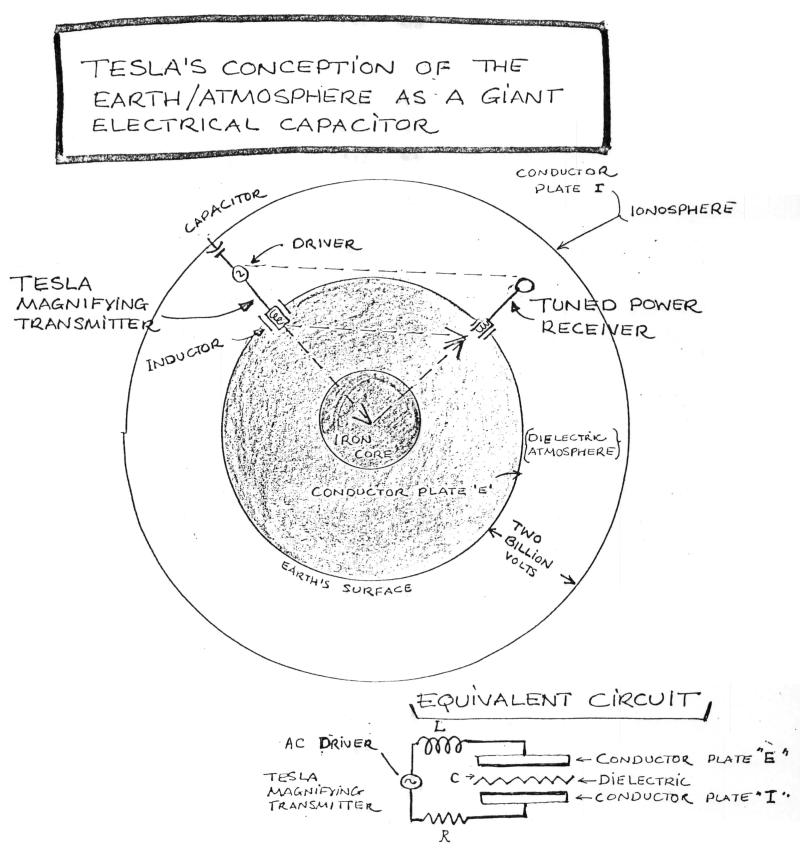
1. The Tesla Magnifying Transmitter (TMT) is an electrical oscillator consisting of a flat horizontal primary inductor L on earth coupled to a secondary, and a capacitor ball C which latter is elevated above the earth plane at a distance which is ¼ the wavelength of the resonant frequency of the system.
2. The LCR system is resonant to the fundamental frequency of the earth/atmosphere which is essentially a giant capacitor system.
3. The TMT generates electrical potentials of the order of 100,000,000 volts peak to peak, with currents of the order of 2-4 KAmps.
4. The TMT broadcasts electrical power (wireless) to the Tesla Magnifying Receiver (TMR) stations at distances of hundreds of miles from the source.
5. Tesla claimed the following effects:
   1. The primary path of the wireless power transmission from TMT to the TMR is through the earth which becomes a conductor of electricity.
   2. The secondary path of the wireless power transmission from TMT to TMR is through the atmosphere to close the circuit.
   3. The electrical power is transmitted at less than 1% loss.
   4. He measured electrical stationary waves in the earth.
   5. He measured signals traversing the earth at velocities 27 times the speed of light, c.
   6. The system as described, and the effects claimed were all verified experimentally by Tesla and his colleagues, in 1904. No one has tried to repeat Tesla's work since 1904.
6. There has been great reluctance on the part of engineers and physicists to accept Tesla's data, largely because such data cannot be reconciled with physical theory in vogue between 1904 to 1976, and the experiments are not easy to repeat.
7. A theoretical explanation of Tesla's data on his TMT is given as follows:

The Lienard-Wiechert solution of the Maxwell equations for electromagnetism show that the propagated EM wave is a time derivative of the velocity, c, known as the retarded potential. In the TMT the retarded potential is identified with the atmospheric radiation of the EM signal from the elevated capacitor ball C. The Lienard-Wiechert solution also shows the existence of a wave faster than c known as the advance potential. Since this is the imaginary solution, and does not have physical detectibility, it is usually ignored. However, if the advance potential is treated by the de Broglie equation as a phase velocity wave we can visualize it as a “hole” or tubular wave guide moving faster than c, for the retarded potential which is slower than c, the two potentials being 180° out of phase.

This “tubular wave guide” can be analyzed by means of the Dirac equation (for the electron) which shows it to be a rotating field with the properties of magnetism and spin. At high voltages, ca. 100 Mev., there is an interaction between the advance potential wave guide field, and the retarded potential photonic field such that particle pairs (electron - positron) are created, or the pairs are annihilated to yield photonic radiation. In dense materials such as that of the earth this reaction is augmented by the presence of atomic nuclei. Thus theoretically the TMT can transfer large amounts of current using the earth as a conductor, and under appropriate conditions of resonance (frequency and voltage) gain (or magnification) of power is feasible.

In order to understand the workings of the Tesla Magnifying Transmitter (TMT), we will present in an elementary form some of the basic concepts of electricity as formulated by Maxwell (from Encyclopedia Brit., V.6, p. 660 ff). We relate electromagnetic radiation to its source by means of the potentials as given in the two Maxwellian equations where:

$!B = Magnetic = Vector Potential (A)$!

$!E = Electric = Scalar Potential (ϕ)$!

$!B = curl A$!

(1)

$!E = - grad ϕ - \frac{∂A}{∂t} (2)$!

The other two Maxwell equations become:

$!▽^2 φ + div \frac{∂A}{∂t} = - ρ / ε_0, (3)$!

$!▽ x (▽ x A) + \frac{1}{c^2} \frac{∂A}{∂t^2} + \frac{1}{c^2} grad \frac{∂φ}{∂t} = μ_0 j (4)$!

The divergence of A and the time derivative of ϕ are not specified by their definitions in terms of the fields, and may be chosen so that,

$!div A + \frac{1∂φ}{c^2∂t} = 0 (5)$!

This is called the Lorentz condition on the potentials. If the Lorentz condition is satisfied, the potentials are solutions of the second-order inhomogenous wave equations,

$!▽^2 φ - \frac{1}{c^2} \frac{∂^2φ}{∂t^2} = - ρ / ε_0, (6)$!

$!▽^2 A - \frac{1}{c^2} \frac{∂^2A}{∂ t^2} = - μ_0 j. (7)$!

The fields excited by the charge ρ, and current j, sources are determined by differentiating the potentials, which are particular solutions of these equations.

It was first shown by Ludvig Valentin Lorenz, a Danish physicist, that solutions may be written formally as volume integrals over the source distributions evaluated at the retarded time,

equal to the time (t) for which the field is described minus the distance travelled (r) divided by the velocity, or

$!t' = t - \frac{r}{c}, (8)$!

which would allow the transmission of the fields from the source with velocity c; that is,

$!φ(x, y, z, t) = \frac{1}{4πε_0} \displaystyle \int \frac{ρ (x', y', z',   t - r/c)}{r} dV', (9)$!

$!A(x, y, z, t) = \frac{1}{4π} \frac{j (x', y', z',   t - r/c)}{r} dV', (10)$!

in which r is the distance from a source point (primed coordinates) to the field point (plain coordinates). These are the retarded potentials; mathematically the advanced potentials, with the integrals evaluated at t + r/c, are equally valid, but in the classical radiation theory physical significance is not attached to such solutions. The reason for this lack of notice of the advanced potentials is that they move at speeds greater than c and therefore cannot be detected by physical instruments all of which operate either at, or below, the velocity of light, c.

The Lorenz advanced potential solution is the key to understanding the Tesla Magnifying Transmitter (TMT).

The TMT has two components where the physical capacitor C, is the source for the scalar potential ϕ; and the physical inductor L, is the source for the vector potential A. The two sources are coupled as a series LC resonator. Resonance is achieved with respect to the earth/air capacitor C' as the load which has a resistive component R. For the TMT to operate and efficiently carry out wireless transmission of electrical energy two conditions must be satisfied: 1) The potential of the TMT must exceed 100,000,000 volts at a resonant frequency for the system L C R. 2) A Tesla Magnifying Receiver (TMR) sharply tuned to the L C R resonant frequency must be placed somewhere on the earth to receive the electrical power of the TMT.

The vector potential A associated with L then takes the form of the advanced potential which propagates through the earth at velocity greater than c. The advanced potential propagates as a rotating “magnetic” field (tangential to line of propagation) which creates a tunnel effect “wormhole” from the TMT to the TMR. The “hole” thus created in advance of the arrival of the retarded potential from the source ϕ, in fact, “directs” the electromagnetic radiation to the TMR where maximum power transfer occurs.

A simple example will show that the retardation is responsible for the existence of the physical electromagnetic fields, which must fall off as the inverse first power of the distance. Likewise, the advance potential is responsible for “tubule” or “wormhole” effects in any media which are in effect rotating “magnetic” fields propagating faster than the speed of light and which increase as the first power of the distance.

If a charge e, is restricted to a small region of space near the origin of coordinates, then, to a first approximation, the vector potential at a large distance r, is simply

$!A (x, y, z, t) = \frac {μ_0}{4π} \frac {ev (t - r/c)}{r} (11)$!

The relation B = curl A requires taking the space derivatives, each term of which would behave as 1/r² at best, except for the fact that the distance r, is also involved in the retarded time. The radiation field is thus proportional to the time derivative of the velocity. When we solve the equation integrals at t + r/c, the radiation power will increase proportionately with distance and velocity as r². The latter solutions must be arrived at relativistically. With respect to the retarded potential, if the motion of the charge is confined to the z axis, the magnetic field is azimuthal, and given by

$!B_φ = \frac {μ_0}{4πc} \frac {qv̇}{r} sin Θ = \frac {1}{4πε_0} \frac {qv̇ sin Θ}{rc^3}. (12)$!

In this simple approximation θ is the angle between the z axis and the line r from source to observer. The corresponding electric vector is along the direction of change in angle θ and equal in magnitude to cB in these units. The exact potentials corresponding to a point charge, in contrast to this approximation are not obtained by substituting the total charge for the volume integral indicated in the retarded potentials.

The problem arises because of the finite velocity of field propagation, so that the integral of the retarded charge density over space is not in general equal to the total charge. Conversely, the advance potential charge density will in general be greater than the total charge, hence the “magnifying” character of the Tesla Transmitter. The correct potentials for an electron of charge e, are

$!φ = \frac {1}{4πε_0} \begin{bmatrix} \frac{e}{R - \mathbf{R} \cdot ν/c} \end{bmatrix}, (13)$!

$!A = \frac {μ_0}{4π} \begin{bmatrix} \frac{eν}{R - \mathbf{R} \cdot ν/c} \end{bmatrix}, (14)$!

in which R is the radius vector from the electron to the field point, ν is the velocity of the electron, and the square bracket is used to denote the fact that all quantities are to be evaluated at the retarded time, not the time of observation. These are known as the Lienard-Wiechert potentials. Before the advent of relativity theory they could not be justified for high-velocity electrons, because it was necessary to assume that Maxwell's equations were valid only in the reference frame of the observer. But the Lienard-Wiechert potentials are relativistically correct, and are also valid for the entire range of classical electrodynamics. The general formula for the rate of radiation from a moving charge, as derived from the Lienard-Wiechert potentials, depends on the velocity as well as the acceleration. This explains why the TMT is only effective if it operates at a potential above 100,000,000 volts which imparts a relativistic velocity (and energy) to electrons,

$!\frac{-dU}{dt'} = \frac{e^2}{6\pi\varepsilon_0 c^3} \frac{(\nu^2 - (\nu \times \nu)^2 /c^2)}{\left(1 - \frac{\nu^2}{c^2}\right)^3} (15)$!

Where U is the total energy of the source, and relativistically, the velocity is interpreted as the relative velocity of the charge e, with respect to the observer, but t' is the retarded time, with respect to which the velocity and acceleration of the source are to be evaluated. Likewise, for the advanced potential solution t' becomes the advanced time, and the relativistic solution is given at 1 + ν²/c².

The expressions for the electric and magnetic fields are complicated except for simple motions, but in all circumstances

$!B = r X \frac {E}{r/c} (16)$!

so that the magnetic field is always perpendicular to the electric field, and to the retarded radius vector from the charge to the field point. For the advanced potential the magnetic field is always 180° to the electric field, and to the radius vector from the field point to the charge. These relationships can be more precisely stated by working more directly with the time derivative of the velocities—both less, and greater than c. In accord with the principles of Fourier analysis, the solutions of the inhomogeneous wave equation may be constructed from components that are harmonic in time, so that the time dependence may be represented by the exponential coefficient

$!e^{-iωt} (17)$!

Here w = 2πv is the angular frequency, and i , is the imaginary number $\sqrt{-1}$. Introducing the factor -iω is equivalent to taking the time derivative of the velocity.

This factor can be broken down by Euler's formula into the sum of two terms, one the real part, and the other the complex part, so called because it contains the imaginary factor i.

The actual fields are to be identified with the real part of the complex field expressions, as obtained by use of the Euler formula

$!e^{-iωt} = cos ωt - i sin ωt, (18)$!

together with the real part of the corresponding formula for the complex factor in the spatial coordinates. To obtain instantaneous values of the energy density and other quantities that depend on the product of field strengths, it is necessary to write the real fields before multiplying, but it is simple enough to find the time average of such products.

The role of advanced potential waves with velocity greater than c was portrayed from a different approach by Louis de Broglie in 1923. He proposed that particles, such as the electron, should have wave properties. He suggested that a particle of mass m₀ at rest and thus having an energy (relativistic) m₀c² also has associated with it a periodic phenomenon of a specific frequency ν₀ = E/h = m₀c²/h. (19)

If it moves relative to an observer with a certain velocity ν, the observer will see the frequency shifted (by the relativistic time dilation defined by the theory of relativity) to a value

$!\nu = \nu_0 (1 - \nu^2/c^2)^½ (20)$!

On the other hand, the energy of the moving particle is such that it would correspond to a frequency

$!\nu = \nu_0 (1 - \nu^2/c^2)^-½ (21)$!

De Broglie proved that these two waves moved so as to be always in phase: the former at the same speed as the particle, i.e., phase wave. He recognized the analogy to a phenomenon of ordinary wave motion in a dispersive medium, that, when a group of waves of slightly different frequencies travel at slightly different speeds, they produce by interference a group wave that travels at a speed significantly different from all of them, and it is the group velocity that represents the speed of transport of energy by the waves.

Making use of this parallel, de Broglie deduced the wavelength, λ, of the matter waves:

$!\lambda = \frac {h}{p} (22)$!

p = momentum of particle

h = Planck's constant

Just as Planck's equation

$!E = hv (23)$!

is the fundamental relationship for light quanta, so the equation

$!\lambda = \frac {h}{p} (24)$!

is the fundamental equation for matter waves.

Given the existence of the advance potential, and its relationship to the phase wave, as related to the transport of energy (retarded potential, and group wave) we ask how the high potentials of the TMT explain power conduction through the earth?

Pair production is a process in which a high energy wave (gamma wave frequencies) is converted into an electron and a positron. The process is described in an electron theory proposed by P. A. M. Dirac through a method of approximation. He envisaged the process as the transition of an electron from a negative to a positive energy state. There is a fraction of residua energy in pair production, symbolized by the Greek letter alpha, α, unexpended in conversion of energy to mass, that appears in any one particle (e.g., the electron). This is given by the kinetic energy of that electron E_e minus its rest energy, mc², divided by the energy of the gamma ray hν, minus twice the rest energy of the electron 2 mc² , or,

$!\alpha = \frac {(E_e - mc^2)}{(h \nu - 2 mc^2)} (25)$!

Because the same equation applies to each of the two electrons that are formed, it must be symmetric about the condition that each of the particles has half the residual energy, symbolized by α (in excess of that conveyed to a “third body”, such as the atomic nucleus); i.e., that α = 0.5. Below an energy of about 10,000,000 electron volts for the gamma ray, the probability for pair production is almost independent of the atomic number of the material; and, up to about 100,000,000 electron volts of energy, it is almost independent of the quantity α. At higher energies, approximately equal to or greater than 100,000,000 electron volts, pair production is the dominant mechanism of radiation interaction with matter.

According to Dirac's “hole” theory all negative energy states are ordinarily filled with electrons, a uniformity that is impossible to detect and which is sometimes called the electron vacuum. A hole in the distribution of negative energy states constitutes the anti-electron, with positive charge and positive energy. The transition of an electron from a negative energy state to one of positive energy results in the creation of a pair. The reverse transition results in the annihilation of a pair. Complications arise from such a quantum theory of the pure radiation field, excluding charges and other sources. Such complications have no counterpart in classical theory, but it is possible to describe a vacuum radiation field in terms of quantized normal modes in such a way that Maxwell's equations are satisfied in the limit of Planck's constant approaching zero (h → 0) in addition to Lorentz covariance as required by special relativity. These normal modes correspond to photons, which individually carry energy, momentum, and angular momentum. In actual physical world particles serve as sources and absorbers for photons. As an example of the complications, the negative energy states of the Dirac theory are affected by the existence of an electromagnetic field (such as high voltage), resulting in what is called the polarization of the vacuum. A constant field produces a constant polarization which would be unobservable; and straight forward attempts to compute its magnitude have led to the embarrassing result that the effect is infinite. Inhomogeneous fields produce finite and observable effects that can be calculated. These complications arose out of the attempt to solve some of the defects of principle in the Schrödinger equation for wave mechanics. For one thing, the spin of the electron was introduced into the equation by Schrödinger on an ad hoc basis; and for another the equation is not in harmony with the theory of relativity. The difficulty arises from the fact that the relativistic expression for the energy, E, of a free particle is

$!E = ±[(cp)^2 + (mc^2)^2]^½ (26)$!

Where m and p are the mass and momentum, respectively of the free particle, and c is the velocity of light. This cannot be used directly, as the square root has no clear meaning once the transition is made to the operators (either Schrödinger's derivatives, or Heisenberg's matrices) of quantum theory.

The problem was solved by Dirac in 1928 by the expedient of setting

$!E = c (\alpha_x p_x + \alpha_y p_y + \alpha_z p_z) + \beta mc^2 (27)$!

in which p_x, p_y, p_z, are the three mutually perpendicular components of momentum, satisfying px² + py² + pz² = p². Here α_x, α_y, α_z, and β are determined by the requirements that they be independent of position and time and that

$!E^2 = (cp)^2 + (mc^2)^2, (28)$!

the same results that would be obtained by squaring both sides of equation (26) above.

The α's and β cannot be ordinary numbers, as the restrictions on them show; a typical one is α_xβ + βα_x = 0.

Rather they turn out to be operators themselves. Moreover, whereas for a classical free particle the orbital angular momentum L is a constant of the motion, this is not true for a particle the energy of which is of the form of equation (27); instead to L must be added a combination of the α's and β. This combination must represent an angular momentum, which does not depend on the motion of the particle, and is therefore an intrinsic angular momentum, or spin. This can be visualized as Tesla's rotating magnetic field (as an advanced potential) in the negative energy state of Dirac behaving like de Broglie's phase wave with respect to the particle state. When the effect of an electromagnetic field is included in the equation, the “spin” is found to have associated with it a magnetic moment (as proposed by Uhlenbeck and Goudsmit). Thus Dirac's proposal solved the two difficulties, and of course historically implied the existence of the electron anti-particle—the positron—which was discovered in 1931.

But the description of particles and radiation is far from complete. The fact remains that no one yet (1976) knows how to write down exactly, in compact form, an equation describing the complete interaction between a proton and an electron, let alone solve it. Thus when we try to explain the operation of the TMT in terms of advance potential theory, phase wave theory, and negative energy state theory, we can only suggest that Tesla's ideas are feasible. Their validity can only be proved in well-designed experiments. It is clear that there is no contradiction between Tesla's data and claims, and that of modern theory.