Nikola Tesla Articles
The Moon's Rotation (Follow-up)
In this article Dr. Tesla proves conclusively by theory and experiment that all the kinetic energy of a rotating mass is purely translational and that the moon contains absolutely no rotational energy, in other words, does not rotate on its axis. — EDITOR.
In revising my article on “The Moon’s Rotation”, which appeared in the April issue of the Electrical Experimenter, I appended a few remarks to the original text in further support and elucidation of the theory advanced. Due to the printer’s error these were lost and, in consequence, I found it necessary to forward another communication which, unfortunately, was received too late for embodiment in the May number. Meanwhile many letters have reached me in which certain phenomena presented by rotating bodies, as the moon’s librations of longitude, are cited as evidences of energy due to spinning motion, i.e., proofs of axial rotation of the satellite in the true physical sense. I trust that the following amplified statement will meet all of the objections raised and convert to my views those who are still unconvinced.
The kinetic energy of a rotating mass can be determined in four ways which are illustrated in diagrams, Figs. 1, 2, 3 and 4 and may be found more or less suitable.
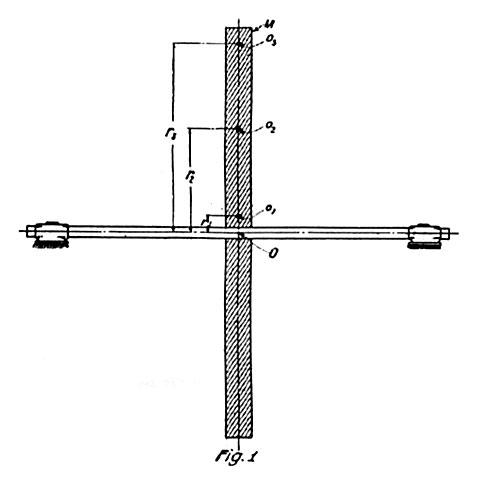
Referring to Fig. 1, the method consists in selecting judiciously a number of points as o1, o2, o3, etc., within the straight rod or mass M, respectively at distances r1, r2, r3, etc., from the axis of rotation O and calculating the square root of the mean square of these distances. Its value being Rg, denoted radius of gyration, the effective velocity of the mass at n revolutions per second will be Vn= 2 π Rg n and its kinetic energy E = ½ M Vn2 = ½ M (2 π Rg n)2.
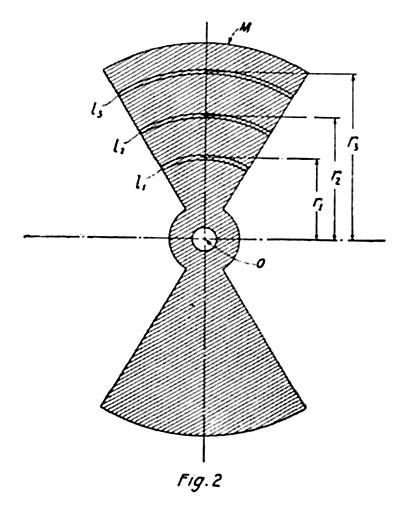
In Fig. 2 the mass M, rotating n times per second about an axis O at right angles to the plane of the paper, is divided into numerous elements or small parts, most conveniently very thin concentric laminae, as l1, l2, l3, etc., at distances r1, r2, r3, etc., from O. Since the kinetic energy of each part is equal to half the product of its mass and the square of the velocity, the sum of all these elemental energies E = ½ Σ m V2 = ½ m1 V12 + ½ m2 V22 + ½ m3 V32 + …… = ½ m1 (2 π r1 n)2 + ½ m2 (2 π r2 n)2 + ½ m3 (2 π r3 n)2 + ……
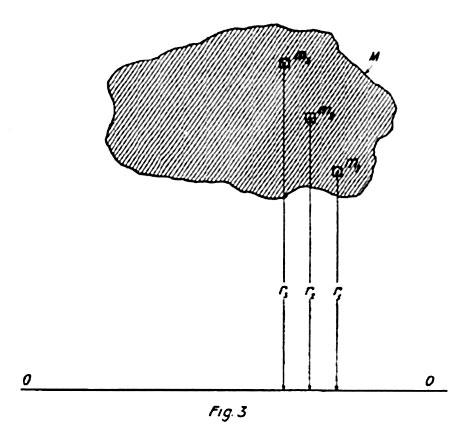
A different form of expression for the energy of a rotating body may be obtained by determining its moment of inertia. For this purpose the mass M (in Fig. 3), rotating n times per second about an axis O, is separated into minute parts, as m1, m2, m3, etc., respectively at distances r1, r2, r3, etc., from the same. The sum of the products of all these small masses and the squares of their distances is the moment of inertia I, and then E = ½ I ω2, ω = 2 π n being the angular velocity.
It is obvious that in all these instances many points or elements will be required for great accuracy but, as a rule, very few are sufficient in practice.
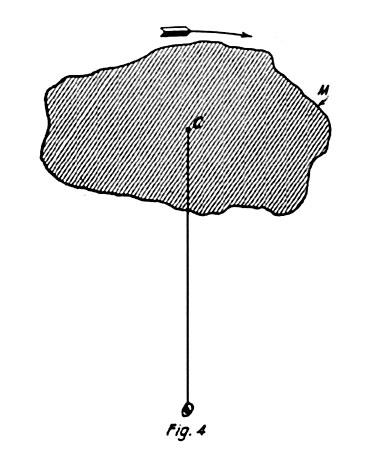
Still another way to compute the kinetic energy is illustrated in Fig. 4, in which case the quantity I is given in terms of the moment of inertia Ie about another axis parallel to O and passing thru the center of gravity C of mass M. In conformity with this the energy of motion E = ½ M V2 + ½ Ie ω2 in which equation V is the velocity of the center of gravity.
The preceding is deemed indispensable as I note that the correspondents, even those who seem thoroly familiar with mechanical principles, fail to make a distinction between theoretical and physical truths which is essential to my argument.
In estimating the kinetic energy of a rotating mass in any of the ways indicated we arrive, thru suitable conceptions and methods of approximation, at expressions which may be made quantitatively precise to any desired degree, but do not truly define the actual condition of the body. To illustrate, when proceeding according to the plan of Fig. 1, we find a certain hypothetical velocity with which the entire mass should move in order to contain the same energy, a state wholly imaginary and irreconcilable with the actual. Only, when all particles of the body have the same velocity, does the product ½ M V2 specify a physical fact and is numerically and descriptively accurate. Still more remote from palpable truth is the equation of motion obtained in the manner indicated in Fig. 4, in which the first term represents the kinetic energy of translation of the body as a whole and the second that of its axial rotation. The former would demand a movement of the mass in a definite path and direction, all particles having the same velocity, the latter its simultaneous motion in another path and direction, the particles having different velocities. This abstract idea of angular motion is chiefly responsible for the illusion of the moon’s axial rotation, which I shall endeavor to dispel by additional evidences.
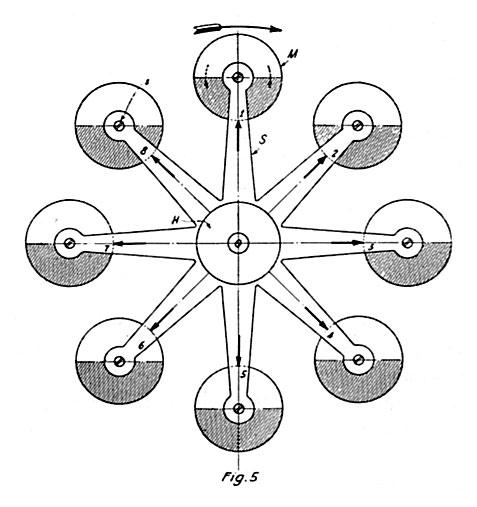
With this object attention is called to Fig. 5 showing a system composed of eight balls M, which are carried on spokes S, radiating from a hub H, rotatable around a central axis O in bearings supposed to be frictionless. It is an arrangement similar to that before illustrated with the exception that the balls, instead of forming parts of the spokes, are supported in screw pivots s, which are normally loose but can be tightened so as to permit both free turning and rigid fixing as may be desired. To facilitate observation the spokes are provided with radial marks and the lower sides of the balls are shaded. Assume, first, that the drawing depicts the state of rest, the balls being rotatable without friction, and let an angular velocity ω = 2 π n be imparted to the system in the clockwise direction as indicated by the long solid arrow. Viewing a ball as M, its successive positions 1, 2, 3-8 in space, and also relatively to the spoke, will be just as drawn, and it is evident from an inspection of the diagram that while moving with the angular velocity ω about O, in the clockwise direction, the ball turns, with respect to its axis, at the same angular velocity but in the opposition direction, that of the dotted arrow. The combined result of these two motions is a translatory movement of the ball such that all particles are animated with the same velocity V, which is that of its center of gravity. In this case, granted that there is absolutely no friction the kinetic energy of each ball will be given by the product of ½ M V2 not approximately, but with mathematical rigor. If now the pivots are screwed tight and the balls fixt rigidly to the spokes, this angular motion relatively to their axes becomes physically impossible and then it is found that the kinetic energy of each ball is increased, the increment being exactly the energy of rotation of the ball on its axis. This fact, which is borne out both by theory and experiment, is the foundation of the general notion that a gyrating body — in this instance ball M — presenting always the same face towards the center of motion, actually rotates upon its axis in the same sense, as indicated by the short full arrow. But it does not tho to the eye it seems so. The fallacy will become manifest on further inquiry.
To begin with, observe that when a mass, say the armature of an electric motor, rotating with the angular velocity ω, is reversed, its speed is -ω and the difference ω – (-ω) = 2 ω. Now, in fixing the ball to the spoke, the change of angular velocity is only ω; therefore, an additional velocity ω would have to be imparted to it in order to cause a clockwise rotation of the ball on its axis in the true significance of the word. The kinetic energy would then be equal to the sum of the energies of the translatory and axial motions, not merely in the abstract mathematical meaning, but as a physical fact. I am well aware that, according to the prevailing opinion, when the ball is free on the pivots it does not turn on its axis at all and only rotates with the angular velocity of the frame when rigidly attached to the same, but the truth will appear upon a closer examination of this kind of movement.
Let the system be rotated as first assumed and illustrated, the balls being perfectly free on the pivots, and imagine the latter to be gradually tightened to cause friction slowly reducing and finally preventing the slip. At the outset all particles of each ball have been moving with the speed of its center of gravity, but as the bearing resistance asserts itself more and more the translatory velocity of the particles nearer to the axis O will be diminishing, while that of the diametrically opposite ones will be increasing, until the maxima of these changes are attained when the balls are firmly held. In this operation we have thus deprived those parts of the masses which are nearer to the center of motion, of some kinetic energy of translation while adding to the energy of those which are farther and, obviously, the gain was greater than the loss so that the effective velocity of each ball as a whole was increased. Only so have we augmented the kinetic energy of the system, not by causing axial rotation of the balls. The energy E of each of these is solely that of translatory movement with an effective velocity Ve as above defined such that E = ½ M Ve2. The axial rotations of the ball in either direction are but apparent; they have no reality whatever and call for no mechanical effort. It is merely when an extraneous force acts independently to turn the whirling body on its axis that energy comes into play. Incidentally it should be pointed out that in true axial rotation of a rigid and homogenous mass all symmetrically situated particles contribute equally to the momentum which is not the case here. That there exists not even the slightest tendency to such motion can, however, be readily established.
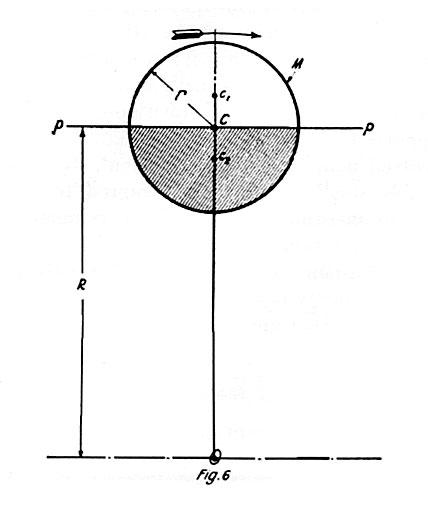
For this purpose I would refer to Fig. 6 showing a ball M of radius r, the center C of which is at a distance R from axis O and which is bisected by a tangential plane pp as indicated, the lower half sphere being shaded for distinction. The kinetic energy of the ball when whirled n times per second about O is according to the first form of expression E = ½ M Ve2 = ½ M (2 π Rg n)2, M being the mass and Rg the radius of gyration. But, as explained in connection with Fig. 4, we have also E = ½ M V2 + ½ Ie ω2, V = 2 π R n being the velocity of the center of gravity C and Ie the moment of inertia of the ball, about the parallel axis passing thru C and equal to 2/5 M i2 so that E = ½ M (2 π R n)2 + 1/5 M r2 (2 π n)2. Neither of these two expressions for E describes the actual state of the body but the first is certainly preferable conveying, as it does, the idea of a single motion instead of two, one of which moreover is devoid of existence. I shall first undertake to demonstrate that there is no torque or rotary effort about center C and that the kinetic energy of the supposed axial rotation of the ball is mathematically equal to zero. This makes it necessary to consider the two halves separated by the tangential plane pp wholly independent from one another. Let c1 and c2 be their centers of gravity, then Cc1 = Cc2 = 3/8 r. In order to ascertain the kinetic energy of the hemispheres we have to find their radii of gyration which can be done by determining the moments of inertia Ic1 and Ic2 about parallel axes passing thru c1 and c2. Complex calculation will be avoided by remembering that the moment of inertia of either one of the half spheres about an axis thru C is Ic = ½ X 2/5 M r2 = 1/5 M r2, and since M = 2 m, Ic = 2/5 m r2. This can be exprest in terms of the moments Ic1 and Ic2; namely, Ic = Ic1 + m (3/8 r)2 = Ic2 + m (3/8 r)2. Hence Ic1 = Ic2 = Ic – m (3/8 r)2 = 2/5 m r2 – 9/64 m r2 = 83/320 m r2. Following the same rule the moments of inertia of the half spheres about the axis passing thru the center of motion O can be found. Designating the moments for the upper and lower halves of the ball, respectively, Io1 and Io2 we have Io1 = m (R + 3/8 r)2 + Ic1 = m (R + 3/8 r)2 + 83/320 m r2 and Io2 = m (R – 3/8 r)2 + Ic2 = m (R – 3/8 r)2 + 83/320 m r2. Thus for the upper half sphere the radius of gyration Rg1 = √ Io1 / m = √ (R + 3/8 r)2 + 83/320 r2 and for the lower one Rg2 = √ Io2 / m = √ (R + 3/8 r)2 + 83/320 r2
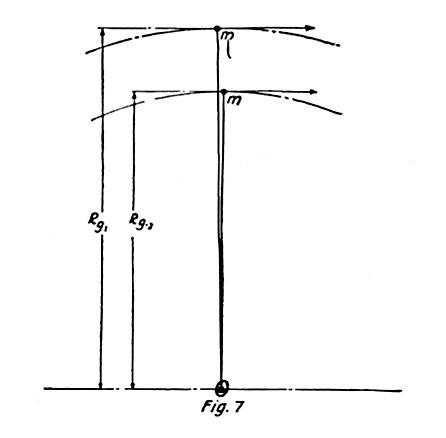
These are the distances from center O, at which the masses of the half spheres may be concentrated and then the algebraic sum of their energies — which are wholly translatory those of axial rotation being nil — will be exactly equal to the total kinetic energy of the ball as a unit. The significance of this will be understood by reference to Fig. 7 in which the two masses, condensed into points, are represented as attached to independent weightless strings of lengths Rg1 and Rg2 which are purposely shown as displaced but should be imagined as coincident. It will be readily seen that if both strings are cut in the same instant the masses will fly off in tangents to their circular orbits, the angular movement becoming rectilinear without any transformation of energy occurring. Let us now inquire what will happen if the two masses are rigidly joined, the connection being assumed imponderable. Here we come to the real bug in the question under discussion. Evidently, so long as the whirling motion continues, and both the masses have precisely the same angular velocity, this connecting link will be of no effect whatever, not the slightest turning effort about the common center of gravity of the masses or tendency of equalization of energy between them will exist. The moment the strings are broken and they are thrown off they will begin to rotate but, as pointed out before, this motion neither adds to or detracts from the energy stored. The rotation is, however, not due to an exclusive virtue of angular motion, but to the fact that the tangential velocities of the masses or parts of the body thrown off are different.
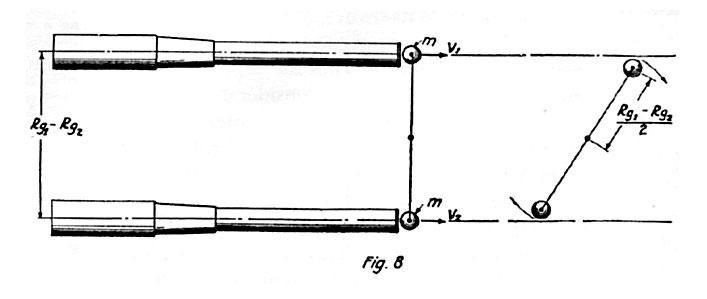
To make this clear and to investigate the effects produced, imagine two rifle barrels, as shown in Fig. 8, placed parallel to each other with their axes separated by a distance Rg1 – Rg2 and assume that two balls of same diameter, each having mass m, are discharged with muzzle velocities V1 and V2, respectively equal to 2 π n Rg1 and 2 π n Rg2 as in the case just considered. If it be further supposed that at the instant of leaving the barrels the balls are joined by a rigid but weightless link they will rotate about their common center of gravity and in accordance with the statement in my previous article above mentioned, the relation will exist V1 – V2 / 2 = π n (Rg1 – Rg2) n being the number of revolutions per second. The equalization of the speeds and kinetic energies of the balls will be, under these circumstances, very rapid but in two heavenly bodies linked by gravitational attraction, the process might require ages. Now, this whirling movement is real and requires energy which, obviously, must be derived from that originally imparted and, consequently, must reduce the velocity of the balls in the direction of flight by an amount which can be easily calculated. At the moment of discharge the total kinetic energy was E = ½ m V12 + ½ m V22 which is evidently equal to m V32, V3 being the effective velocity of the common center of gravity, from which follows that V3 = √ V12 + V22 / 2. The speed of revolution of the masses is, of course, V1 – V2 / 2 and the rotational energy of both balls, which must be considered as points, is e = m (V1 – V2 / 2). The kinetic energy of translation in the direction of flight is then ½ m V12 + ½ m. V22 – m (V1 – V2 / 2)2 = m (V1 + V2 / 2)2 = m V42, V4 = V1 + V2 / 2 being the speed of the common center of gravity, so that V3 – V4 is the loss of velocity in the direction of flight owing to the rotation of the two mass points. If instead of these we would deal with the balls as they are, their rotational energy e1 = e + i ω2 = m (V1 + V2 / 2)2 + i (2 π n)2, i being the moment of inertia of each ball about its axis.
As will be seen, we arrive at precisely the same results whether the movement is rectilinear or in a circle. In both cases the total kinetic energy can be divided into two parts, respectively of the same numerical values, but there is an essential difference. In angular motion the axial rotation is nothing more than an abstract conception; in rectilinear movement it is a positive event.
Virtually all satellites route in like manner and the probability, that the acceleration or retardation of their axial motions — if they ever existed — should come to a stop precisely at a definite angular velocity, is infinitesimal while it is almost absolutely certain that all movement of this kind would ultimately cease. The most plausible view is that no true moon has ever rotated on its axis, for at the time of its birth there must have been some deformation and displacement of its center of gravity thru the attractive force of the mother planet so as to make its peculiar position in space, relative to the latter, in which it persists irrespective of distance, more or less stable. In explanation of this, suppose that one of the halls as M in Fig 5 is not of homogenous material and that it is similarly supported but on an axis passing thru its center of gravity instead of form. Then, no matter in what position the ball is fixed on the pivots, its kinetic energy and centrifugal pull will be the same. Nevertheless a directive tendency will exist as the two centers do not coincide and there is, consequently, no dynamic balance. When permitted to turn freely on the axis of gravity the body, of whatever shape it may be, will tend to place itself so that the line joining the two centers points to O and there may be two positions of stability but, generally, if the center of gravity is not greatly displaced, the heavier side will swing outwardly. Such condition may obtain in the moon if it had solidified before receding from the earth to great distance, when the arrangement of the masses in its interior became subject to gravitational forces of its own, vastly greater than the terrestrial. It has been suggested that the planet is egg-shaped or ellipsoidal but the departure from spherical form must be inconsiderable. It may even be a perfect sphere with the centers of gravity and symmetry coinciding and still rotate as it does. Whatever be its origin and past history, the fact is, that at present all its parts have the same angular velocity as though it were rigidly connected with the earth. This state must endure forever unless forces from without the luna-terrestrial system bring about different conditions and thus the hope of the star-gazers that its other side may become visible some day must be indefinitely deferred.
A motion of this character, as I have shown, precludes the possibility of axial rotation. The easiest way to free ourselves of this illusion is to conceive the satellite subdivided into minute and entirely independent parts, as dust particles, which have different orbital, but rigorously the same angular, velocities. One must at once recognize that the kinetic energy of such an agglomeration is solely translational, there being absolutely no tendency to axial rotation. This makes it also perfectly clear why the moon, provided its distance does not greatly increase, must always turn the same face to us even without any inherent directive tendency nor so much as the slightest effort from the earth.
Referring to the librations of longitude, I do not see that they have any bearing on this question. In astronomical treatises the axial rotation of the moon is accepted as a material fact and it is thought that its angular velocity is constant while that of the orbital movement is not, this resulting in an apparent oscillation revealing more of its surface to our view. To a degree this may be true, but I hold that the mere change of orbital velocity, as will be evident from what has been stated before could not produce these phenomena, for no matter how fast or slow the gyration, the position of the body relative to the center of attraction remains the same. The real cause of these axial displacements is the changing distance of the moon from the earth owing to which the tangential components of velocity of its parts are varied. In apogee, when the planet recedes, the radial component of velocity decreases while the tangential increases but, as the decrement of the former is the same for all parts, this is more pronounced in the regions facing the earth than in those turned away from it, the consequence being an axial displacement exposing more of the eastern side. In perigee, on the contrary, the radial component increases and the effect is just the opposite with the result that more of the western side is seen. The moon actually swings on the axis passing thru its center of gravity on which it is supported like a ball on a string. The forces involved in these pendular movements are incomparably smaller than those required to effect changes in orbital velocity. If we estimate the radius of gyration of the satellite at 600 miles and its mean distance from the earth at 240,000 miles, then the energy necessary to rotate it once in a month would be only ( 600 / 240,000 )2 = 1 / 160,000 of the kinetic energy of the orbital movement.