Nikola Tesla Articles
The Tesla Longitudinal Wave
George W. Damm suggests that Nikola Tesla incorporated acoustic resonant criteria in the design and modulation of his tower at Shoreham, Long Island. At first, this seems a bit farfetched, but a pause to check the dimensions of the tower’s components and their acoustic resonant frequencies reveals that they are well-matched to the earth’s electrical resonant frequencies. Tesla’s sensitivity to sound, vibration and light, and his early work with compressed air oscillator frequency control may have been combined in his last major project.
When reading this report, do so with the physics of acoustic vibrations in mind; that is, ordinary sound waves in air. Sound waves are longitudinal in nature and propagate in the form of compression and rarefaction in a medium, at the speed of sound. The speed of sound in standard air is 340 meters/sec (1115 feet/sec). Nikola Tesla insisted his electrical transmissions were longitudinal in nature, and thus similar to sound waves. Whereas sound waves have compression (-) and rarefaction (+), electrical waves have positive and negative charge polarity.
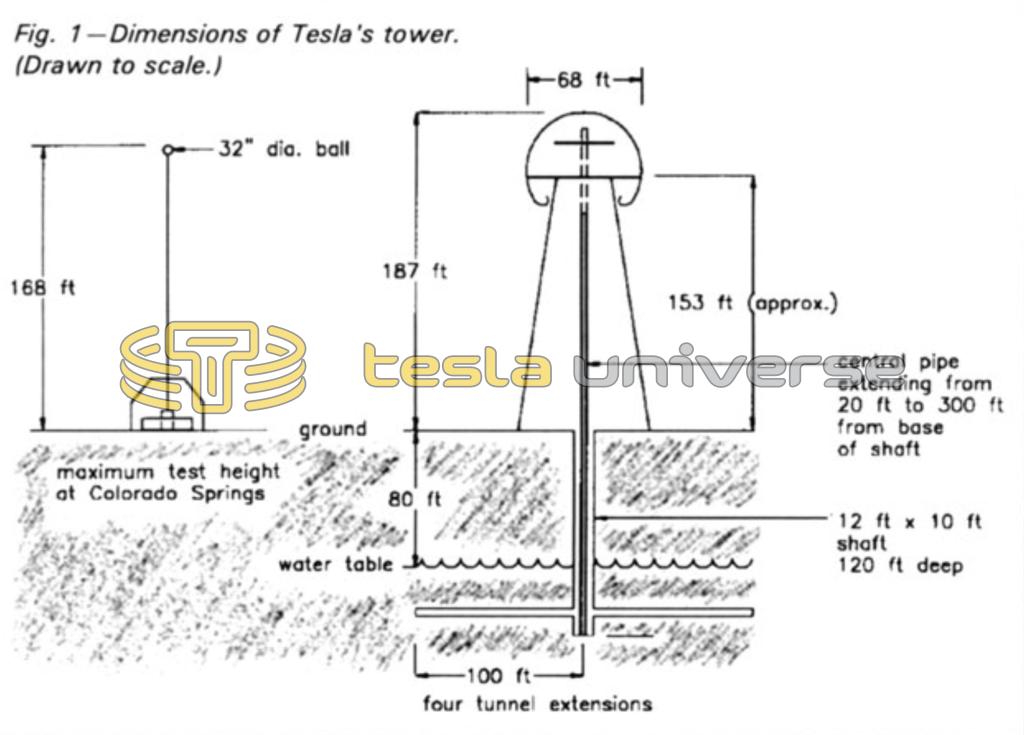
In order to show how Tesla may have incorporated actual acoustic vibration into the tower’s design, some descriptions and dimensions of the tower will be helpful.1 These are shown in Figure 1.
By Tesla’s own testimony1, the tower was 187 feet tall from the ground to the top of the dome. The shaft into the ground was 10 x 12 feet square and 120 feet deep. The water table was reached at a depth of 80 feet. Other sources2 state that four smaller diameter shafts were bored below water level at the base of the main shaft, each with a length of 100 feet and perpendicular to each other. These provided an intimate electrical contact to the earth.
The dome on top of the tower is given to have a diameter of 68 feet. The dome framework was constructed completely of steel. It sat on top of the tower truss structure which was made entirely of pine timbers and steel plates at the joints. A segmented steel pipe telescoped to extend up to 300 feet from the base of the underground shaft. There were about 16 telescoping sections. The variable heights were used to determine the nodal points for electrical vibrations. Tesla said he could measure any distance on earth with an accuracy of ± four feet, including the earth’s size.1
For the dimensions of the tower given in Figure 1, it is possible to calculate various fundamental acoustic frequencies and their harmonics. Key dimensions of the tower are shown in Table 1.
| Dome diameter | 68 ft | 20.7 m |
| Tower height to dome top | 187 ft | 57.0 m |
| Tower height to mid-dome | 153 ft | 46.6 m |
| Shaft depth | 120 ft | 36.6 m |
| Telescoping tube length | up to 300 ft | up to 91.5 m |
| Depth to water table | 80 ft | 24.4 m |
| Table 1 — Dimensions of Tesla’s tower. | ||
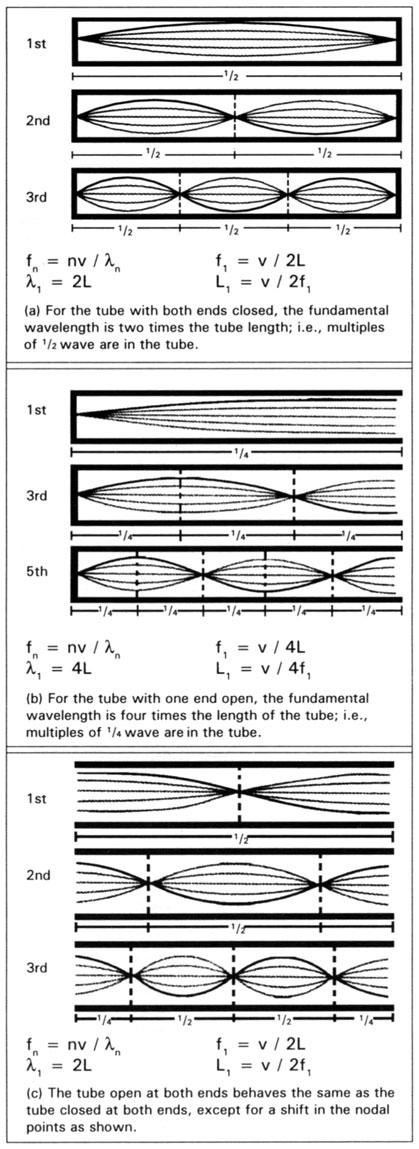
The acoustic resonant frequency and nodal points for pipes differ somewhat depending on whether the pipe is closed at both ends, has one end open, or is open at both ends. The manner in which this varies is shown in Figure 2.3
Given the various dimensions (L) of the tower design and the velocity of sound (v = 340 m/sec = 1115 ft/sec), it is possible to calculate various acoustic fundamental and harmonic resonant frequencies. Upon doing this, it is evident that the air acoustic resonant frequencies of the tower fall in the same range as the earth electrical resonant frequencies. For example, the telescoping tube length (L) can be calculated for a couple of earth electrical resonant frequencies that have been mentioned on occasion. One resonant frequency mentioned is 7.5 Hz. The fundamental frequency (f1) is given by:
(f1) = v / λ1 . (1)
The fundamental wavelength (λ1) is therefore given by:
λ1 = v / f1. (2)
If Tesla used a closed telescoping tube, in order to adjust to the first fundamental wavelength node, it would need to be extended to a length (L):
L = v / 2f1 . (3)
L = v / 2f1 = (340m/sec) / (2 x 7.5 cyc/sec) = 22.7m = 74.3 ft.
This is the node-to-node half wavelength of the fundamental frequency illustrated in Figure 2a.
If the telescoping tube were open at one end, the first fundamental node-to-node length (L) would be:
L = v/4f1 . (4)
L = 340 / (4 x 7.5) = 11.3m = 37.2 ft.
The acoustic wavelength (λ1) is 4L or 148.7 ft. This is shown in Figure 2b.
Tesla mentions the period of 0.08484 seconds for an electric pulse to travel the earth’s diameter and back. This is approximately an 11.79 Hz pulse rate.
For the closed tube, the fundamental tube length (L) for an 11.79 Hz pulse rate would be:
L = 340 / (2 x 11.79) = 14.4m = 47.3 ft,
λ = 2L = 94.6 ft.
For the telescopic tube open on one end, the fundamental length (L) would be:
L = 340 / (4 x 11.79) = 7.2m = 23.7 ft,
λ = 4L = 94.6 ft.
The higher harmonics all require longer tube lengths, which are readily allowed with the telescoping tube’s ability to extend 300 feet.
The similarity of the numerical values for acoustic and electrical resonant frequencies provides a basis for the argument that Tesla may have incorporated acoustic compression and rarefaction techniques into the process of modulating the electrical waves propagated and received at the dome.
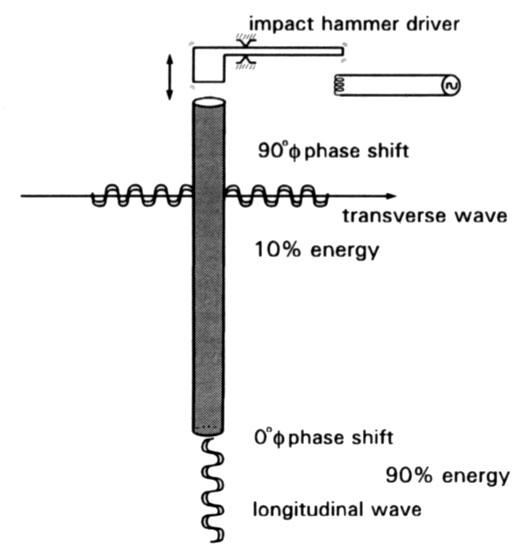
I think that Tesla used the term Φ phase not in relation to time, but rather to polarity. The term Φ phase may therefore be used in reference to negative polarity (-) for compression and positive polarity (+) for rarefaction. Perhaps when Tesla talked about frequency it was in relation to impulses per second and not sine wave cycles. This translates to (electrostatic and kinetic) pressure for negatlve impulses on molecules for compression, or a vacuum for positive impulses on molecules for rarefaction.
I think what Tesla intended was conversion from electrical to vibrational acoustic resonance and resonators (as indicated in Figure 3). His coils and towers were not only electrical, but also acoustic and vibrational. In my opinion, he had learned how to convert transverse waves to longitudinal waves and vice versa.
The hole in the ground was perhaps not only a ground-plane, but an organ pipe tuned to a beat frequency of 12 cycles per second. By changing the beat frequency he was able to shift the Φ phase between compression and rarefaction.
When he was in Colorado, I think Tesla was trying to tune in to the resonance of the earth’s magnetic field, which is connected to a natural static charge existing in the atmosphere. Perhaps he acoustically modulated this earth capacitance such that it would magnify all effects. Therefore, his hole in the ground and telescoping pipe at Shoreham were used as an acoustic resonator, like an organ pipe.
When two charged bodies are separated, the work of separating them increases the difference in their potential. I believe that Tesla used acoustic modulation to produce such voltage increases. Such induction may represent a principle source of charge separation in clouds.
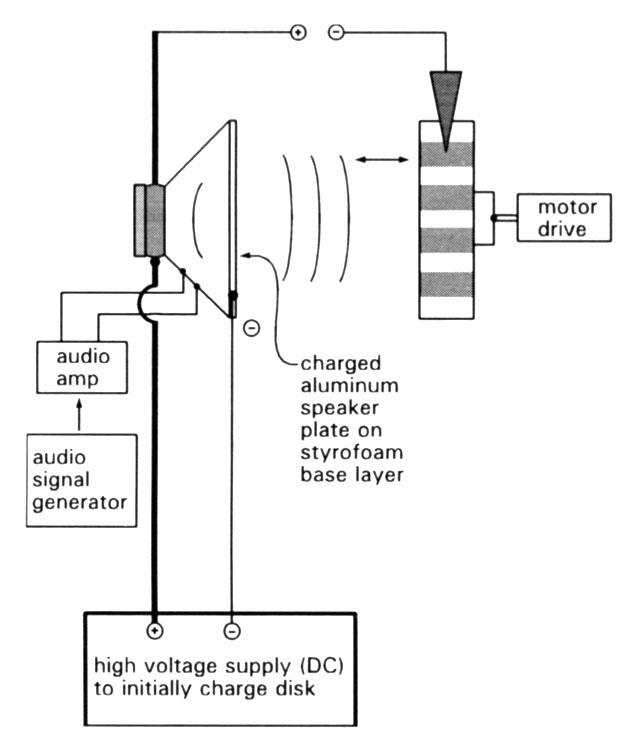
Figure 4 shows my idea of an acoustically modulated electrostatic charge.
References
1. Leland Anderson. Nikola Tesla On His Work With Alternating Currents and Their Application to Wireless Telegraphy, Telephony, and Transmission of Power. Denver: Sun Publishing, 1992.
2. Natalie Aurucci-Stiefel. “Looking Back at Rocky Point.” Series of five articles. Community Journal, Wading River, NY: Nov. – Dec. 1994.
3. Wave design adapted from Physics For Scientists and Engineers. 3rd ed., vol. 1. by Paul A. Tipler. New York: Worth Publishers, 1976: 421, 457.
George Damm is currently retired with an active focus of interest relating to Tesla’s work, magnetic imaging, plasma, magnetics and electrostatics. He has worked as a technician in radio, TV, radar, electronic sensors and magnetic imaging. He has spent much of his research activity with the RCA tube division. Rockefeller Institute, Princeton Plasma Physics Lab, Tokomak, General Instruments and the State University of New York at Stony Brook. Damm lives near the Shoreham, Long Island site of Tesla’s Wardenclyffe Tower.