Nikola Tesla Books
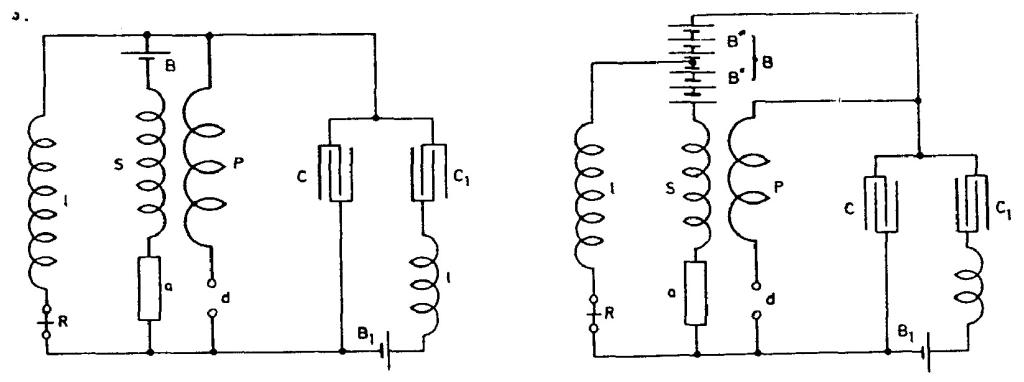
In Diagram 2. two condensers C and C1 are placed in series, one of them being shunted by graduated self-induction l and battery B1. The other condenser C, being larger, allows the current from battery B to pass through break and coil l when device a is excited. Not very good. A modified plan is illustrated in 3. In this case the auxiliary battery B1 charges the two condensers C and C1 in series, whereupon one of them is discharged through the break d. This is fair.
In 4. the battery (main) is so placed that a high e.m.f. is charging the condenser yet current through the sensitive device is small.
Colorado Springs
Aug. 11, 1899
Measurement of capacity of the new condensers prepared from Maniton Water bottles.
With the exception of three tanks in which bottles with green glass were used all the remaining bottles were of dark glass. The test did not show much difference between the two kinds of glass and all the tanks separately measured were found to be, after proper filling in of the solution, of the same capacity or very nearly so. All the bottles were first connected in quantity and the capacity compared with that of 1/2 mfd. standard condenser. The deflections were almost exactly as 36:44, 36° for the 1/2 mfd. and 44° for the bottles. The capacity of all the latter was therefore $! {11 \over 18} $! = 0.611 mfd. This would give for one bottle, since there were 576 bottles, the average value of $! {11 \over {18 \times 576}} $! = 0.00106 mfd. or 0.00106 x 9 x 105 = 955 cm. As there are 36 bottles in each of the tanks we get for one tank 36 x 0.00106 = 0.03816 mfd. or 36 x 955 = 34,380 cm. As each side has 8 tanks the capacity of each side would be 0.03816 x 8 = 0.30528 mfd. or 275,040 cm. and when, as mostly the case, the two sides are in series the total primary capacity will be $! {0.611 \over 4} $! = 0.15275 mfd. or 0.15275 x 9 x 105 = 137,475 cm. When working with one primary turn, taking the inductance of primary as $! {7 \over 10^{4}} $! henry we get
$! {T = {{2 \pi \over 10^{3}} \sqrt{0.15275 \times {7 \over 10^{5}}}} = {2.054 \over 10^{5}}} $! and n = 48,700 per sec.
145
Tesla: âApparatus for utilizing effects transmitted from a distance to a receiving device through natural mediaâ, U.S. Patent 685 955, Nov. 5, 1901, Appl. Sep. 8, 1899, P-312.