Nikola Tesla Books
varied until resonance of free system comprising coil of 400 t. and ball of 38.1 cm cap. was obtained. This was evident from spark length and other indications, as streamers.
Results:
| Ball position | Capacity in primary on each side | Turns in self. box | Spark gap primary | Spark second. | The experiments were interrupted here because of darkness |
|---|---|---|---|---|---|
| lowest | 1 old + 3 2/3 new tanks | 22 | 1/2" + 1 turn | 53" | |
| 2 feet higher | 1 old + 4 1/3 " | 22 | " | " |
From this computed found that by elevating 2 feet, capacity was increased by a ratio of !$ {{\text{5 1/3} \over \text{4 2/3}} = {16 \over 14} = {8 \over 7}} !$ or about 15% nearly, really 14.3%. This is a value found nearly the same before in previous tests.
To be followed up.
205
October 4
Tesla was primarily interested in the change of capacity of a ball with height, so he measured the primary capacity for two elevations of the ball. In both cases he tuned for resonance of a "special coil". In the first measurement he had Lp Cp1 = Lsc Cb1 = 1/Ï21 and in the second Lp Cp2 = Lsc Cb2 = 1/Ï22, where p refers to the primary circuit and b to the ball. These equations neglect the effect of interaction between the primary and secondary. They readily yield Tesla's equation
!$ {Cp_{1} \over Cp_{2}} = {Cb_{1} \over Cb_{2}} !$
The inductance of the primary Lp and of the "special coil" Lsc do not figure in the capacity ratio equation. In deriving this equation all distributed capacitance in the secondary and the secondary coil itself are neglected.
October 4
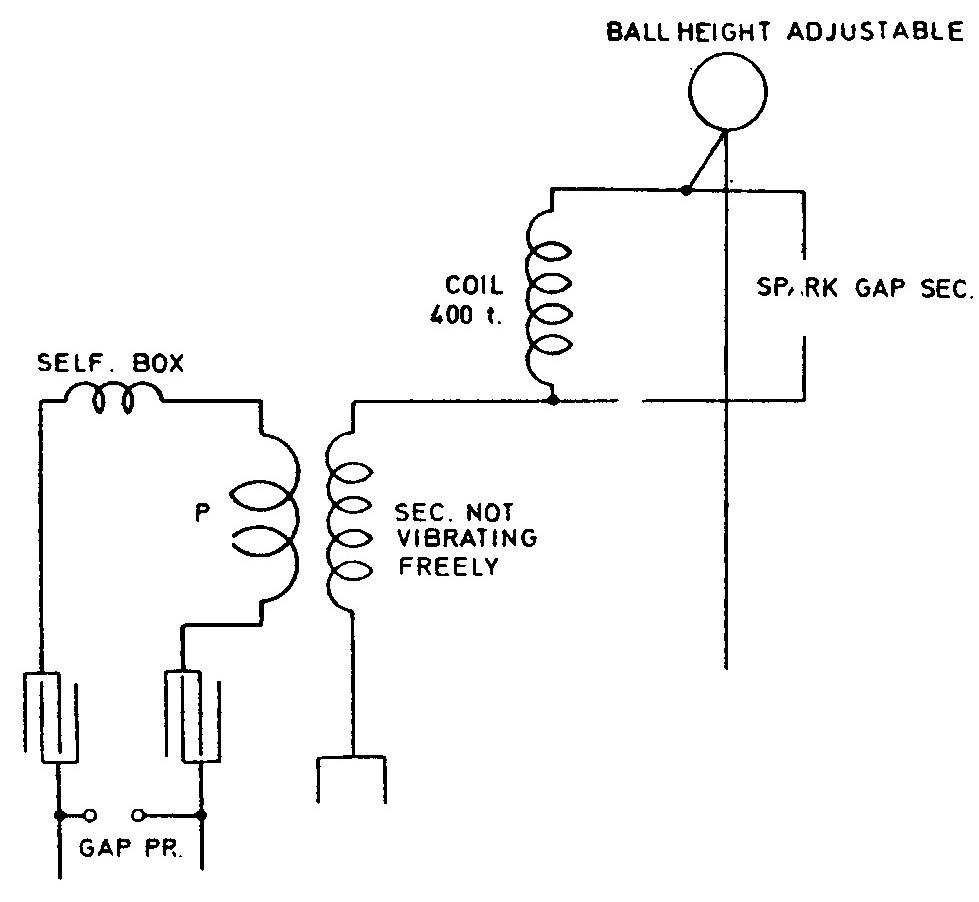
He performs the experiments in order to determine the variations of capacitance.of and isolated metal body at various distances from the ground surface. He constructs the ''special coil'' which is connected between the secondary and the globe. He particularly makes efforts to reduce the internal coil capacitance.
The oscillator frequency is reached by common method by adjustment of regulating coil and capacitor in the primary circuit. The maximum voltage (i.e., the longest spark on terminal of "special coil") is the indication of adjusted oscillator. For the secondary he enters the note on the figure that it does not "vibrate freely". Tesla is particularly interested in globe capacitance variations due to height. Because of that he performs two primary capacitance measurements for the two globe positions. In both cases he achieves the resonance on "special coil". In the first measurement the relation is LpCp1 = LscCk1 = !$ {1 \over {Ï_{1}}^{2}} !$, and in second LpCp2 = LscCk2 = !$ {1 \over {Ï_{2}}^{2}} !$
These equations do not take into account the mutual influence of the primary and secondary on the oscillator operation. On the basis of the above equations it is easy to get Tesla's equation !$ {C_{p1} \over C_{p2}} !$ = !$ {C_{k1} \over C_{k2}} !$, where the index p is related to primary circuit and index k to the sphere. Lp (primary inductance) and Lsc ("special coil" inductance) do not enter in the equation for the capacitance relationship. When developing the last equation all distributed capacitances in the secondary are neglected as well as the secondary coil itself.