Nikola Tesla Books
Colorado Springs
Oct. 21, 1899
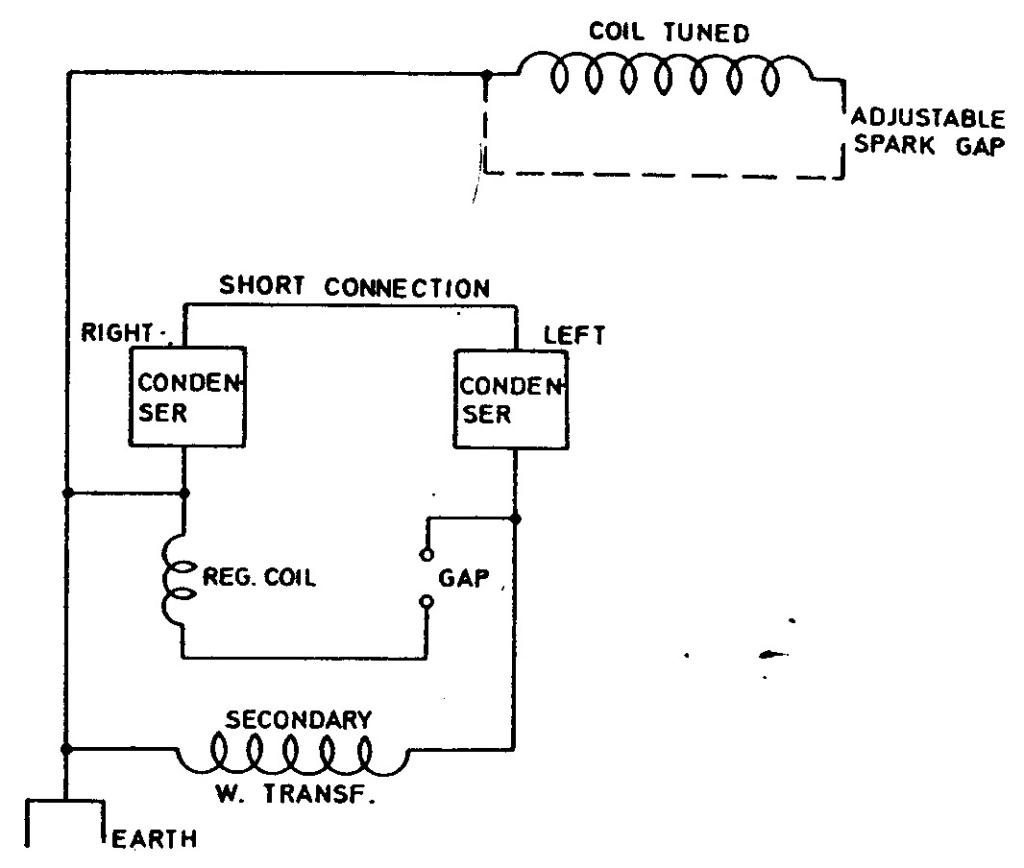
To ascertain the value of connections in terms of turns of the regulating coil and for other purposes the coil before described, 404 turns with rubber wire attached, was tuned for three different values of the regulating turns. The method was one frequently used in New York and is illustrated in the plan shown. One end of the coil was connected to that end of condensers, or respectively to that end or terminal of transformer which was grounded and the rise of potential of free terminal of tuned coil was observed by an adjustable spark gap. In this manner very close adjustments are easy. The resonating condition indicated by the longest sparks in the adjustable gap was secured with the following three values:
| Capacity in the primary in bottles on each side | Turns in regulating coil |
|---|---|
| total | |
| 8 tanks less 2 bottles = 286 = 0.15157 | 16.5 |
| 7 less 2 " = 250 = 0.13249 | 18 = L1 |
| 6 " 2 " = 214 = 0.11341 | 21 = L2 |
The tuning was not quite as sharp in the first case, but it was very sharp in the last two experiments. Taking these and calling x the self-induction of the connections we would have in the case corresponding to L1 of the regulating coil !$ {T = {2 \pi 10^{3}} \sqrt{0.13249 (L_{1} + x)}} !$ and in the case corresponding to L2 of the self-induction coil
!$ {T = {{2 \pi \over 10^{3}} \sqrt{0.11341 (L_{2} + x})}} !$.
From this 0.13249 (L1 + x) = 0.11341 (L2 + x) and
!$ {x = {{0.11341 L_{2} - 0.13249 L_{1}} \over 0.01908}} !$
Now L1 and L2 should be exactly measured; resonance method will probably suit the purpose best. This is to be more rigorously carried out.
In the experiments before described, for the purpose of ascertaining the influence of elevation on the capacity of a sphere, the latter was connected to the coil of 404 turns by means of a wire No. 10 heavily covered with rubber (3/8" wall). Evidently this wire affected the period of the system and to ascertain to what extent, the wire was placed in
231
October 21
In a thorough analysis of all details of his measuring apparatus, Tesla did not omit a determination of the parasitic inductance of the connections, by an interesting method which he says he used often in the New York laboratory. Varying the primary inductance and capacitance but keeping a constant frequency of the oscillator (as determined with an auxiliary resonant circuit), one has
Cp1(Lp1 + Lcon) = Cp2(Lp2 + Lcon)
where Cp1, Lp1 are the first and Cp2, Lp2 the second capacitance-inductance pair in the primary giving the same frequency. From this equation one can find the parasitic inductance of the connections Lcon, which Tesla denotes by x.
October 21
He studied all details of the measurement apparatus very carefully and Tesla did not neglect to calculate the parasitic inductances in the connections. On Oct. 21 he describes the interesting method (which he claims he frequently applied in the New York laboratory) by means of which the parasitic inductance is determined of the circuit element connections. By variation of inductance and capacitance in the oscillator primary at constant oscillator frequency, (which is determined by means of auxiliary circuits) it could be written: Cp1(Lp1 + Lcon.) = Cp2(Lp2 + Lcon.), where Cp1, Lp1 are the first pair and Cp2, Lp2 are the second pair of capacitances and inductances (of the coils) in the primary circuit.
The inductance of the connections is determined from this equation and that value Tesla designates by X. In the measurement circuit the resonant coil play the role of frequency indicator.
Tesla comes up with the first measured value of sphere capacitance. First he finds the value of the coil and supply connections capacitance, and then the capacitance of the coil, supply connections and the sphere. The measurement method is similar to the one of October 9.