Nikola Tesla Books
With the additional coil of 1500 cm. capacity added in series with secondary on free terminal, the capacity would be 1500 + 290 = 1790, that is about 6 times as much as before. The vibration will then be slower $! {\sqrt{6}} $! = 2.5 approx. times slower, about 37,400 per sec. This better suited.
Colorado Springs
June 29, 1899
The first good trial of a new wound secondary with 36 turns was made today. The wire was No. 10 cord, the turns being wound in every third groove. The distance of wires is approx. 1 7/8".
Vibration under the conditions of the first experiments: Approximate self-induction of secondary about 5x107 cm. Additional coil connected to free end of secondary, the coil having 240 turns, spool 6 feet long, 2 feet diam. Estimated self-induction of coil roughly 107 cm.
A = 2900 sq.cm. l = $! { {2900 \times 240^{2} \times 4 \pi} \over {183}} $! = $! { {576 \times 29 \times 10^{4} \times 12.57} \over {183}} $! =
N = 240 turns
l = 183 cm. = 1140 x 104 = 114 x 105 for rough approximation = 107
The wave length should be (ignoring capacity):
4 x [5280 (sec) + 1440 (spool)] = 4 x 6720 = 26,880 feet or about 5 miles.
To give this wave length the primary vibration should actually be 187,000 : 5 = 37,400 per sec. (same number before found).
The capacity Cp in primary to be found:
$! { {1 \over 37,400} = {2 \pi \over 1000} {\sqrt{LC_{p}}} = {\sqrt{ {7 \times 10^{4} \times C_{p}} \over 10^{9} }} = {2 \pi \over 10^{3}} {\sqrt{ {7 \times C_{p} \over 10} }} } $!
$! {{1 \over 374} = {2 \pi \over 10^{3}} \times 0.84 \sqrt{C_{p}} } $! , $! {\sqrt{C_{p}} = {10^{3} \over {2 \pi \times 0.84 \times 374}} = {1000 \over 1975}} $! or 0.5 approx.
Cp = 0.7 mfd
This would require $! {0.7 \over 0.003} $! jars = 233 jars with two primary turns in multiple and $! {233 \over 4} $! or about 58 jars total with two primaries in series. As so many jars were not available evidently only a higher vibration was obtainable. This explains why first results unsatisfactory.
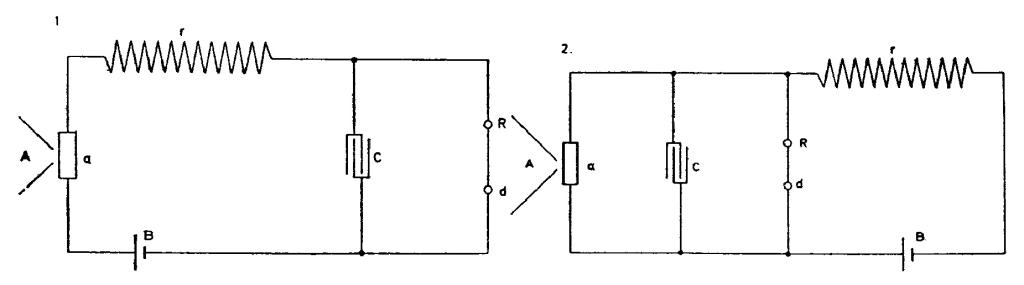
Arrangements of apparatus experimented with in carrying out condenser method. (This for Curtis application)
50
June 28
After four days he again continues the calculations related to transmitter. He calculates the capacitance and inductance of transformer secondary on coil frame with twenty turns on the basis of known values for a coil with 36 turns. Here it is seen that the secondary coil capacitance he considers is proportional to the number of turns and inversely proportional to the distance between turns. Therefore he obtains that the ratio between distributed capacitance of the new coil and distributed capacitance of the old coil is equal N1d/Nd1 (N is the number of turns and d is distance between turns).
The ratio of secondary coils' inductances at number of turns change is calculated from the relation
$! {{\left({N_{1} \over N}\right)^{2} {l \over l_{1}}} = {{\left({N_{1} \over N}\right)^{2}}{Nd \over N_{1}d_{1}}} = {N_{1} d \over Nd_{1}}} $!
Such ratio originates from the equation for an indefinitely long coil and the end result is the same as the one for the ratio of secondary distributed capacitances change.
Numerical data for old coil distributed capacitance appears here for the first time without any explanation. With calculated distributed capacitance and inductance for new coil, Tesla determines the oscillation period for the new secondary. This period (or its reciprocal value - frequency) compares with value obtained on the basis of the condition that wirelength in the secondary coil is equal to quarter of a wavelength. Then he adds the sphere capacitance to secondary and determines the reduction of resonant frequency. He concludes that vibration is high, because then small capacitance in primary circuit is required. In that case the source does not have to operate at full power. At the end, in series with the secondary he adds "additional coil", adds together all capacitances (obviously incorrectly) and by not taking into account the inductance of "additional coil", he determines the change of secondary resonant frequency.
June 29
He didn't use yesterday's calculation, because he continued with a secondary with 36 turns. First detailed tests of oscillator operation did not provide expected results and Tesla attempts to determine the reasons by calculation. He gives secondary inductance, calculates the "additional coil" inductance but he doesn't use these results; then he determines free secondary vibration from the condition that total secondary wire length is equal to one quarter of wavelength. As he is already aware that the capacitances in the secondary circuit change this condition on secondary wirelength, he says in the calculation that the capacitances are neglected. With an approximate value for secondary resonant frequency he determines the required capacitance in primary circuit.
As he used small capacitances in the experiment, he concludes that he operated with high harmonics and that was the reason why he didn't achieve success.
The next day he gave several schematics of receivers with which he experimented probably for the purpose of patent submission preparation. Leonard E. Curtis is the person who appears several times pertaining to Tesla's patents as witness (please see e.g. (8,10)), or as lawyer on several patents starting in April, 1896.