Nikola Tesla Books
vantageously. He will furthermore recognize at once that the simplest form of such a coil, and also the cheapest, will be one with one single layer and, settling upon this form, he will get an approximate estimate as to the diameter of the coil to be adopted. This will, of course, depend much on the kind of wire he uses and particularly on the insulation, since the better the insulation the closer will be two points of the coil between which there will exist a certain maximum pressure. Granted now the diameter of the coil to be constructed is settled upon, it will be at once seen that, assuming turns are wound on until resonance is obtained, the inductance of the coil and the capacity of the same will vary in the like manner. If more turns are wound on the drum their number will be proportionate to the length of the coil, therefore to the length of the wire, and the inductance will be proportionate - on the one hand, to the square of the turns or respectively to the square of the length of the wire, and on the other hand, it will be inversely proportionate to the length of the coil. Inasmuch as this length is likewise proportionate to the length of the wire, the inductance, on the whole, will be proportionate to the ratio $! {l^{2} \over l} $! or to l, that is to say, the inductance of the coil, as more turns are wound on, will grow as the of the wire. And so will also, and obviously, the distributed capacity. And furthermore, and for the same reasons, under the conditions considered, both the capacity and the inductance of the coil will vary inversely as the distance of the turns which I shall designate Ï. This is clear since, as far as the inductance of the coil is concerned, the number of turns will be inversely as Ï, and the length of the coil directly as Ï, hence the inductance will be inversely as Ï; and, as regards the distributed capacity, it will be, of course, inversely proportionate to Ï. Hence we can express both the unknown quantities L and C1 (distributed capacity) in terms of l and Ï. But it should be remembered that in the equation LC = $! {1 \over p^{2}} $!, C is capacity associated with the coil on the free terminal and not the distributed capacity. In case, therefore, we should make the capacity on the free terminal very large in comparison with the distributed capacity of the coil, or if capacity be associated with the coil in other ways, as by shunting the coil with a condenser as in sketch 3. - or in any other way, but so that the distributed capacity may be neglected, then the design of the coil is much simplified, for then one of the constants, preferably C, can be adopted beforehand and the other constant calculated. It will be in such case better to adopt first a capacity, because it is easy to get an idea of what kind of condenser to use when the
pressure of the terminals of the coil is approximately known. A practical way is, sometimes, to adopt a construction before suggested, securing a negligible internal capacity, consisting of the placing of condensers in series with the turns of the coil, and then merely calculating one of the constants, assuming first a value for the other constant, whichever is the more
81
Tesla: âOn light and other high frequency phenomenaâ, a lecture delivered before the Franklin Ins. Philadelphia, Febr. 1893, L-107.
July 11
By introducing the additional coil in the oscillator circuit Tesla achieved one modification of his oscillator with resonant transformer. by which means he obtained higher voltages. When these voltages exceeded several hundred thousand volts, he had to carefully lay out the elements, and choose very good insulators. Here the instructions are given how to make the terminals in order to obtain longest and most powerful spark along with delaying the flashover to the instant when maximum voltage is reached (or some desired voltage). He suggests the procedure which enables the voltage measurement by means of metal spheres of various radii. He discusses the disadvantages of this method because the spheres introduce additional capacitance which disturbs the resonance conditions in high frequency circuits.
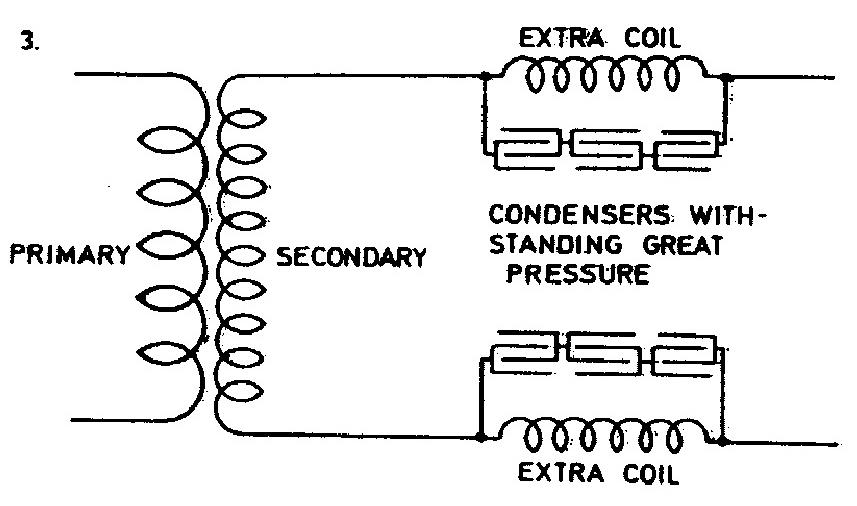
Tesla considers the additional coil extraordinarily suitable for the achievement of "any" voltage. He gives two wiring schematics of this coil for an oscillator high frequency transformer. He claims that with this coil. considerably higher voltages are achieved than with the secondary in poorer linkage with the primary.
Tesla explains this with the fact that the additional coil is not in an inductive link with the primary, and there is no such reaction in the primary which would dampen the oscillation. He doesn't explain how he imagines this coil to be excited and not to react on the primary transformer secondary to which it is directly connected.
The additional coil description is very detailed. Tesla's wealthy experience in coil design is obvious in its full extent. At the end of his considerations he gives the equation for determination of the number of turns for the additional coil on the basis of operation frequency, wire diameter, separation of windings, and a constant which he determines on the basis of experimental results. He checks the equation on one example and obtains a result very close to the experimental results.